東北地方太平洋沖地震記録による表層地盤のモデル同定解析－株式会社バイブラントシステム開発
株式会社 バイブラントシステム開発
Vibrant System Development Co.,Ltd
地盤の適用例：数値モデル同定解析結果
地盤に対して仮定した数値モデルは、質点系モデルです（解析例
には一次元波動方程式に従うモデルによる結果を紹介しています）。 解析は、 東北地方太平洋沖地震（2011年3月11日、M=9.0）の記録に対して「時間領域のモード解析」を適用して求められた伝達関数を参照して実施しました。物性値は、比較的精度良く推定可能な 単位体積重量と層厚を固定して、せん断波速度と減衰係数をパラメータに設定しました。図9に物性値の
初期値Vs0および同定値Vsを示します。
解析より求められた同定値の初期値に対する最大変化率は、上から３番目の層のせん断波速度の+0.88です。 他の物性値は±0.04以下に留まります。変化率
は正常に収束した結果であり、ボーリング調査のバラツキを示すものです。図12は伝達関数の比較図です。EW成分についても同様に良好な結果が得られました。数値モデル同定解析は、わずかな情報（地震記録など）を使用して行うことが多いため常に正規方程式の特異性が問題になります。特異性の特徴的な現象としてパラメータの発散が挙げられます。通常、評価対象関数に対する感度量（微分係数）の相対的に小さいパラメータは発散します。本解析では、変化率が±0.04以下に留まったパラメータがその候補になりますが、弊社で開発した修正特異値分解法により特異性が解消され、それら変動は抑えられました。伝達関数は、斯かるパラメータを大きく変えてもほとんど変化をしません。従って、感度量が小さく、情報に関与しないパラメータの最確値は初期値であると言えます。
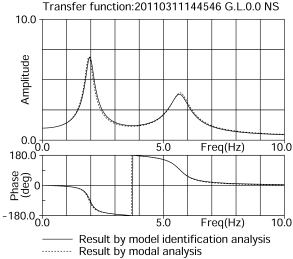
図12 数値モデル同定解析による伝達関数の比較
PDFファイル解析例をご覧いただくためにはAdobe社のAdobeReaderが必要です。最新バージョンの
AdobeReaderは下記アイコンをクリックすることによりダウンロードできます。
